摘要
我们知道价格变化的速度本身就在变化,传统简单均线受困于固定周期参数,这使得不论市场的走势如何,短期均线灵敏度高,更贴近价格走势,但在市场震荡时期反复转向,造成频繁发出错误开平仓信号;长期均线在趋势判断上更加可靠,但在市场加速上涨或下跌时反应迟钝,造成错过最佳的买卖点。
因此虽然传统简单均线可以在一定程度适应行情,但是却很难根据市场变化去进行调整,进而更好的把握趋势。特别在长期震荡行情中,不仅得不到正收益而且付出高额的交易成本,为了解决这个问题,我们引入考夫曼创立的自适应均线。
考夫曼均线
在《精明交易者》中,作者考夫曼(Kaufman)提出了“自适应移动平均线”,简称AMA。该均线考虑到了市场价格变化速率,在普通均线的基础上增加了平滑系数,并自适应动态调整均线的灵敏度,可以在慢速趋势和快速趋势之间自我调整。当市场出现盘整、趋势不明显时期,AMA倾向于慢速移动平均线。当市场波动较大,趋势明显,价格沿一个方向快速移动时,AMA倾向于快速移动平均线。
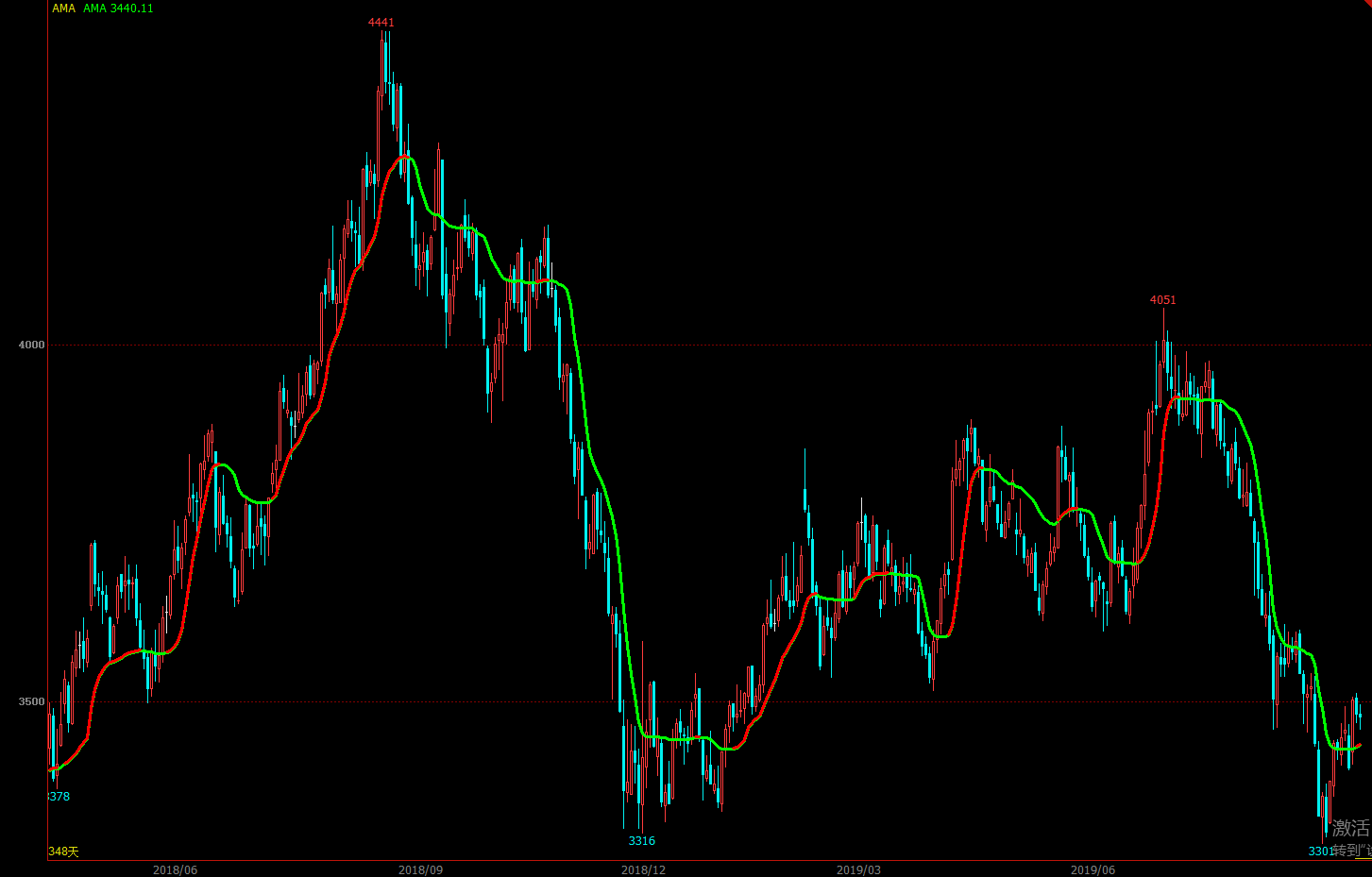 考夫曼均线本质上是根据一段时间内的价格波动率进行调整,计算出了合适的入场阈值提供了最佳的买卖点位。也就是说,它分为两部分主逻辑,第二部分逻辑在波动率层面做了又一次自适应。从而反应市场真实的趋势,便于快速抓住趋势性上涨和下跌的时机,同时规避市场来回震荡的影响。
考夫曼均线本质上是根据一段时间内的价格波动率进行调整,计算出了合适的入场阈值提供了最佳的买卖点位。也就是说,它分为两部分主逻辑,第二部分逻辑在波动率层面做了又一次自适应。从而反应市场真实的趋势,便于快速抓住趋势性上涨和下跌的时机,同时规避市场来回震荡的影响。
考夫曼均线计算
有经验的交易者都习惯于在趋势展开的行情中使用快速均线,在震荡较多的行情中使用慢速均线。但如何把这个方法数量化,让程序来区分这两种行情?这里就需要引入“效率”的概念。
如果价格一致朝一个方向运行,每天收盘价的变化贡献于总的运行幅度,那么就被称为高效率;如果价格涨涨跌跌,很多次收盘价的变化相互抵消,那么就被称为低效率。这类似于物理学中的位移,如果价格在10天内上涨了100个点,我们可称为高效率,如果价格在10天内上涨了10个点,我们可以称为低效率。
第一步:计算价格效率
价格效率是建立在市场移动的速度和方向以及市场中噪声量的基础之上的,假设价格效率是在0~1之间,0表示市场没有移动,只有噪声;1表示市场只有移动,没有噪声。如果价格在10天内上涨了100个点,每天移动10个点,其价格效率就是:100 / (10 * 10) = 1;如果价格在10天内上涨了10个点,但每天震荡10个点,其价格效率就是:10 / (10 * 10) = 0.1
其计算公式是:首先计算价格变动值,即当根K线价格与前N根K线的价格差的绝对值;然后计算价格波动值,即N根K线内,所有价格变动绝对值的总和;最后计算效率系数,即价格变动值除以价格波动值。
- 价格变动值 = abs(价格 - n 日前价格)
- 价格波动值 = sum(abs(价格 - 上一个交易日价格),n)
- 效率系数 = 价格变动值 / 价格波动值
由此可见,在价格变动值一定条件下,市场波动越大,效率系数越小,此时使用慢速移动平均线更能把握整体趋势走向,因为慢速平均线不易被市场短期波动改变方向;反之,价格变动值一定条件下,市场波动越小,效率系数越大,此时应该使用快速(短期)移动平均线。
第二步:计算平滑系数
考夫曼用一系列的移动平均速度来描述平滑系数,其计算方式与EMA类似,根据价格所占权重,重新定义快速和慢速趋势速度系数,比如可以将2天的平均称为快速,30天的平均称为慢速。其中快速趋势系数是:2 /(2 + 1)= 2 / 3 = 0.66667;慢速趋势系数是:2 /(30 + 1) = 2 / 31 = 0.06452。它们的差值是:0.60215。
- 快速趋势系数 = 2 / (n1 + 1)
- 慢速趋势系数 = 2 / (n2 + 1)
上面公式中的n1和n2是交易周期数,并且n1小于n2。默认n1为2,n2为30。最后利用效率比率计算平滑系数,也就是:效率系数 * 0.60215 + 0.06452。
- 平滑系数 = 效率系数 * (快速 - 慢速) + 慢速
可见,当市场波动越大,趋势明显时,平滑系数更加趋向于选择快速趋势系数快速趋势系数,反之,在市场震荡盘整,趋势不明显时期,平滑系数更趋向于选择慢速趋势系数慢速趋势系数。
第三步:计算AMA值
因为在效率系数太低时,可能会取消交易,所以卡夫曼建议在计算AMA值之前,对最后的平滑系数再次乘方。
- 系数 = 平滑系数 * 平滑系数
- AMA = 上一个交易日的AMA + 系数 * (价格 - 上一个交易日的AMA)
假设昨天的AMA值是40,当前的价格是47,它们之间有7个点的差值。那么在一个高效市场,其AMA值提高将近3.1个点,这几乎是差值的一半。在一个低效市场,这个差值几乎不会对AMA值产生影响。
策略逻辑
根据考夫曼的观点,AMA相当于平滑指数,如果其方向改变就应该立刻交易。换句话说就是AMA上升时应该买进,AMA下降时应该卖出。不过如果贸然以此做交易信号,可能会造成大量的无效信号,因此就需要增加一个合适的滤网,即增加另一根AMA均线,以双均线交叉的形式发出买卖信号。
- 多头开仓:AMA1和AMA2均为向上,并且AMA1大于AMA2。
- 空头开仓:AMA1和AMA2均为向下,并且AMA1小于AMA2。
- 多头平仓:AMA1和AMA2均为向下,或者AMA1小于AMA2。
- 空头平仓:AMA1和AMA2均为向上,或者AMA1大于AMA2。
按照以上计算AMA的逻辑,先用代码把它实现出来,首先是计算价格效率:
DIRECTION:=CLOSE-REF(CLOSE,10);
VOLATILITY:=SUM(ABS((CLOSE-REF(CLOSE,1))),10);
ER:=ABS(DIRECTION/VOLATILITY);
然后计算平滑系数:
FASTSC:=2/(2+1);
SLOWSC:=2/(30+1);
SSC:=ER*(FASTSC-SLOWSC)+SLOWSC;
最后计算AMA1和AMA2的值:
AMA1:EMA(DMA(CLOSE,CONSTANT),2),COLORGREEN,LINETHICK3;
AMA2:EMA(DMA(CLOSE,CONSTANT),10),COLORGREEN,LINETHICK3;
有了AMA1和AMA2和值,就可以轻松把策略逻辑实现出来了:
AMA1 > REF(AMA1, 1) && AMA2 > REF(AMA2, 1) && AMA1 > AMA2, BK;
AMA1 < REF(AMA1, 1) && AMA2 < REF(AMA2, 1) && AMA1 < AMA2, SK;
BKVOL > 1 && AMA1 < REF(AMA1, 1) || AMA2 < REF(AMA2, 1) || AMA1 < AMA2, SP;
SKVOL > 1 &&AMA1 > REF(AMA1, 1) || AMA2 > REF(AMA2, 1) || AMA1 > AMA2, BP;
总结
本文构建了自适应均线,并从细节上逐行阐述其中的原理和算法,最后又以双自适应均线创建一个简单的CTA策略。整体来看,与普通均线相比,AMA大大增强了灵活性和使用效率。AMA本意上是用来替代普通均线,以更好地拟合市场价格走势,单独一根AMA并没有质的提升,所以需要额外配置一个过滤器,这个过滤器的选择基于市场波动状况来选择。
(*backtest
start: 2015-02-22 00:00:00
end: 2019-10-18 00:00:00
period: 1h
exchanges: [{"eid":"Futures_CTP","currency":"FUTURES"}]
args: [["SlideTick",2,126961],["ContractType","rb000",126961]]
*)
DIRECTION:=CLOSE-REF(CLOSE,10);
VOLATILITY:=SUM(ABS((CLOSE-REF(CLOSE,1))),10);
ER:=ABS(DIRECTION/VOLATILITY);
FASTSC:=2/(2+1);
SLOWSC:=2/(30+1);
SSC:=ER*(FASTSC-SLOWSC)+SLOWSC;
CONSTANT:SSC*SSC;
AMA1:EMA(MA(CLOSE,CONSTANT),1),COLORGREEN,LINETHICK3;
AMA2:EMA(MA(CLOSE,CONSTANT),10),COLORGREEN,LINETHICK3;
AMA1 > REF(AMA1, 1) && AMA2 > REF(AMA2, 1) && AMA1 > AMA2, BK;
AMA1 < REF(AMA1, 1) && AMA2 < REF(AMA2, 1) && AMA1 < AMA2, SK;
BKVOL > 1 && AMA1 < REF(AMA1, 1) || AMA2 < REF(AMA2, 1) || AMA1 < AMA2, SP;
SKVOL > 1 &&AMA1 > REF(AMA1, 1) || AMA2 > REF(AMA2, 1) || AMA1 > AMA2, BP;
AUTOFILTER;