交易中的数理，你关心的都在这里！

「交易是一门艺术，事关对经济的分析、政策的判断、人性的理解；又是一门严谨的科学，事关随机微积分、概率统计、优化理论。本文从量化金融的起源开始，还原整个体系的建立、发展与完善的历史过程，带你走进算法金融的世界…」

算法本身千差万别，难以一概而论。常见的有以均价为基准的 VWAP；通过固定时间间隔执行的 TWAP； 趋势跟随的 momentum trader 等等。如果你自己编一个根据 MACD，RSI 什么的产生指标的东西，也可以勉强称为 algorithm 。

VWAP 算法 VWAP 算法是一种拆分大额委托单，在约定时间段内分批执行，以期使得最终买入或卖出成交均价尽量接近这段时间内整个市场成交均价的交易策略。其目的是最小化冲击成本，并不寻求最小化所有成本。它是量化交易系统中常用的一个基准。作为一个基准量，VWAP 就是一个计算公式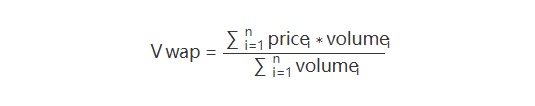： VWAP 算法根据历史成交量，未来的成交量预测、市场动态总成交量，拆单的时间段等因素，把母单分割成为许多小的子单，并在一个指定的时间段内逐步送出去。这样做的效果就是降低了大单对市场的冲击，改善了执行效果；同时增加了大单的隐秘性。显然，VWAP模型的核心就是如何在市场千变万化的情况下，有的放矢地确定子单的大小、价格和发送时间。

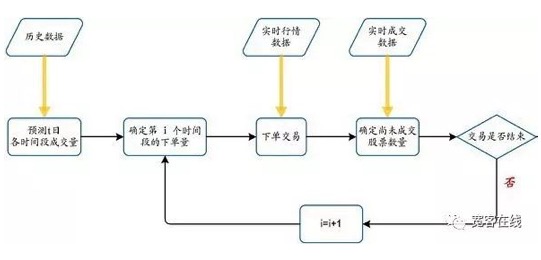
TWAP 算法 与 VWAP 不同的是，TWAP 算法是把一个母单的数量平均地分配到一个交易时段上。该模型将交易时间进行均匀分割，并在每个分割节点上将拆分的订单进行提交。例如，可以将某个交易日的交易时间平均分为N 段，TWAP 策略会将该交易日需要执行的订单均匀分配在这 N 个时间段上去执行，从而使得交易均价跟踪 TWAP，也是一个计算公式：

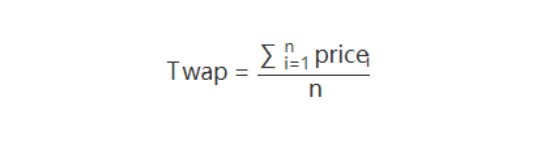
TWAP 并不考虑成交量的因素，而是根据交易时段的平均价格，从而达到减小交易成本的目的。在分时成交量无法准确估计的情况下，该模型可以较好地实现算法交易的基本目的。

但是使用 TWAP 过程中的一个问题是，在订单规模很大的情况下，均匀分配到每个节点上的下单量仍然较大，当市场流动性不足时仍可能对市场造成一定的冲击。

布朗运动 作为 Quant 你不可能不知道布朗运动吧？不仅如此，布朗运动这种 “ 随机游走 ” 的理念贯穿许多科学领域，尤其是普遍运用于各种不可预测的连续时间过程的机制。基于布朗运动的对数正态随机游走理论也是金融市场的经典框架。

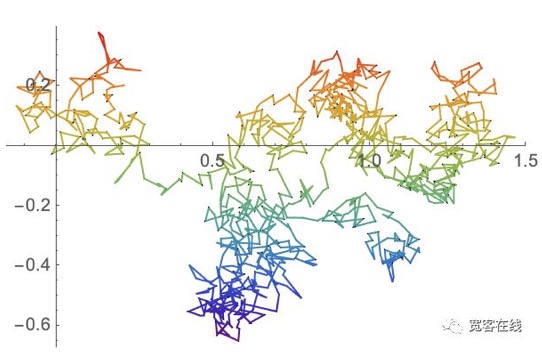
尽管影响股票价格涨跌的原因是无穷无尽的，但价格的运动并非是 “ 完全随机游走 ” 。而是每个因素的影响力通常被反馈力牵制（索罗斯的反身性），市场不但有正反馈机制，还有负反馈机制。

正因如此，很多情况下，价格会有各种正负反馈机制并存，导致正态分布建模的前提不再成立。所以说，价格是一个带着 “ 漂移 ” 的布朗运动。

马尔科夫过程 在概率论及统计学中，马尔可夫过程是一个具备了马尔可夫性质的随机过程。马尔可夫过程是不具备记忆特质的。换言之，马尔可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。

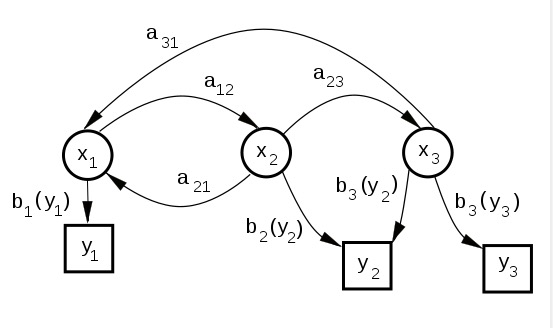
它的时点前和时点后的取值是相互独立的——也就是说，下一分钟发生的事情，完全不受历史时期的变动所控制，只和现在的状态值有关。这样的一个无记忆性的过程给了我们一个事实上的优势——我们在做未来的预测的时候，完全可以不用去看历史价格，而只关注当前价格。

由于这样预测的数据具有不确定性，所以预测结果必然也就是一个概率分布的形式。

假设豆粕在时间 n 的价格为 Sn，对于下一个时点 n+1 而言，其价格 Sn+1 的条件概率并不取决于时点n之前的历史价格，即：

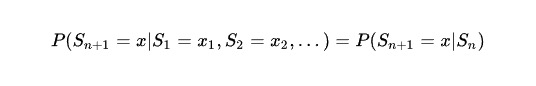
这样S1，S2，S3，…，Sn，… 是一个马尔科夫过程。其中 xi 是一个状态价格，其取值的范围叫做状态空间。当然连续的马尔科夫过程和连续随机变量一样：

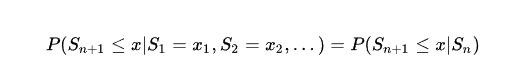
维纳过程 在数学中，维纳过程是一种连续时间随机过程。又与物理学中的布朗运动有密切关系。金融数学中，维纳过程可以用于描述期权定价模型。

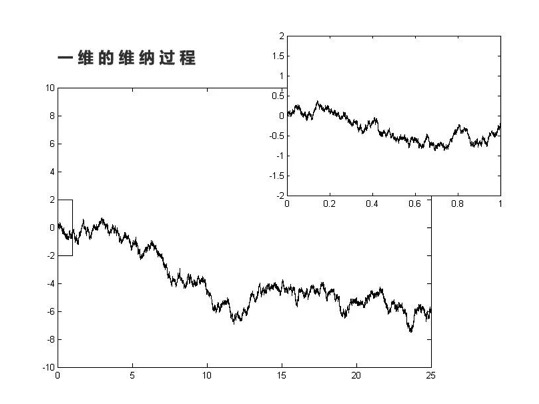
如果一个马尔可夫过程中，增量的概率分布服从于一个关于时间 t 的正态分布，我们就说这个过程是维纳过程，或者说布朗运动。表示成这个样子：

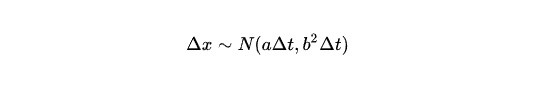
维纳过程本身也是伊藤过程的一个特殊形式，它是包含在伊藤过程这个概念里面的。维纳过程可以用随机漫步或任意拥有平稳独立增量的离散随机过程的尺度极限来构造。这个构造方法基于 Donsker 定理。

伊藤引理 很难想象如果金融学领域没有了维纳过程或者伊藤引理会是怎样的？有些人甚至认为金融学就是伊藤微积分。

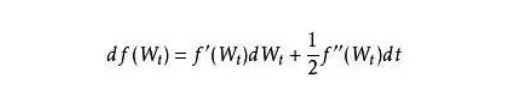
伊藤证明了独立变量随机微分方程和该变量函数的随机微分方程之间的关联，其中一个经典的衍生品定价理论就是资产价格演变的对数正态随机微分方程，伊藤引理告诉我们了该资产期权价格的随机微分方程。

抛硬币（假如这枚硬币的正面和反面一样重），正面朝上我们赢1元，反面我们输1元。当我们抛了N次（次数足够多），我们截取第N-1次抛硬币所有情况的结果，就会发现结果总是符合正态分布。

你要知道每次，抛硬币都是一个独立的事件，每次结果都跟上一次或者下一次以及其他任何一次的结果无关。这就是说我们从布朗运动得到了一个维纳过程。

如果我们把价格分解为：预期收益和波动率两个部分。如果预期收益率和波动率是确定的，就可以用随机变化来表示价格的变化。这就是大名鼎鼎的 Black-Scholes 期权定价模型。

自回归条件异方差模型 在时间序列模型中，ARCH 模型能准确地模拟时间序列变量的波动性的变化，它在金融工程学的实证研究中应用广泛，使人们能更加准确地把握风险（波动性），尤其是应用在风险价值（Value at Risk）理论中，在华尔街是人尽皆知的工具。

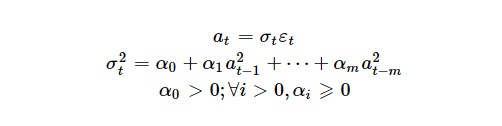
ARCH 模型将当前一切可利用信息作为条件，并采用某种自回归形式来刻划方差的变异。对于一个时间序列而言，在不同时刻可利用的信息不同，而相应的条件方差也不同，利用 ARCH 模型，可以刻划出随时间而变异的条件方差。

另外，还有很多扩展的或改进的模型如求和 GARCH、GARCH-M 模型、指数 GARCH、EGARCH 模型等等。 对于波动率模型，还有比较常用的有随机波动率模型等， 有兴趣可以去研究下。

概率论 作为统计学的数学基础，概率论对诸多涉及大量数据定量分析的人类活动极为重要。概率论是研究随机性或不确定性等现象的数学。交易亦是一种概率游戏。

获得某件事概率值的方法是通过对该事件进行大量相互独立的随机试验，针对每次试验均记录下绝对频率值和相对频率值。随着试验次数的增加，相对频率值会趋于稳定，相对频率值趋向于这个极限值。这个极限值被称为统计概率，表示为：

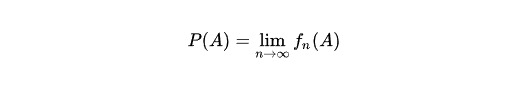
例如，若想知道在一次掷骰子的随机试验中获得 6 点的概率值可以对其进行 3000 次前后独立的扔掷试验，在每一次试验后记录下出现 6 点的次数，然后通过计算相对频率值可以得到趋向于某一个数的统计概率值。

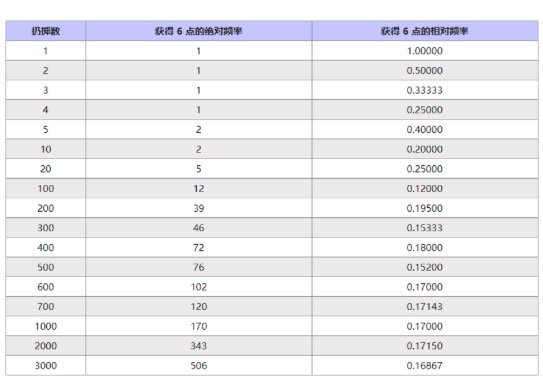
交易中最大的错误在于认为存在能够 100% 地把握行情的可能，认为绝对性的因果关系是存在的，由于混沌系统的存在，由于分形的市场根本特征，所以这种完全的因果关系并不是简单地存在。

每一种方式和交易的技巧都存在不完善性，这是由人的有限理性和认知偏差导致的。正是由于这种缺陷的不可避免，才存在交易技巧的永无止境地提高的可能性。

作者 ：

Hukybo